الجذور التربيعية ، تعرف على الجذور التربيعية ، معلومات عن الجذور التربيع
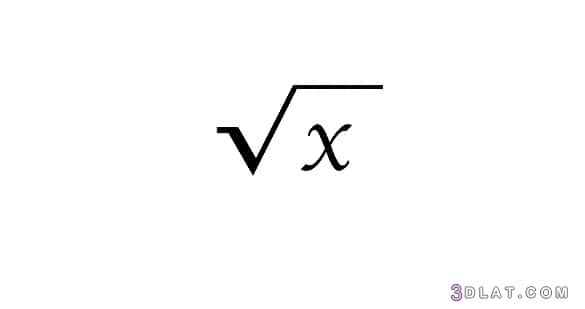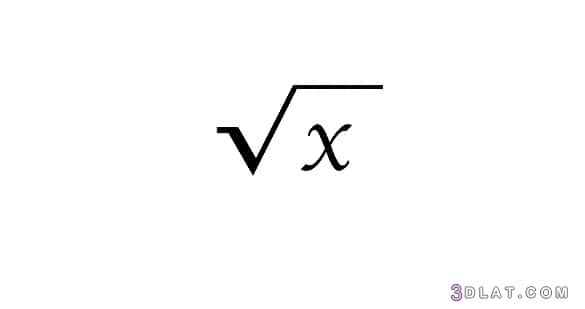
قالو في الرياضيات: “من تعلّم القرآن عظمت قيمته، ومن نظر في الفقه نبل مقداره، ومن تعلّم اللغة رقّ طبعه، ومن تعلم الحساب جزل رأيه ومن كتب الحديث قويت حجته، ومن لم يصن نفسه لم ينفعه علمه”. الرياضيات مهم في فهم الفروع الأخرى من المعرفة، فجميعها تعتمد على الرياضيات بطريقة أو بأخرى، ولا يوجد هناك علم أو مجال إلا وكانت الرياضيات مفتاحاً له، وإن إتقان أي علم يرتبط بدرجة كبيرة بحجم الرياضيات التي ينتفع بها، فالرياضيات هي دعامة الحياة المنظمة ليومنا الحاضر، وبدون الأعداد والدلائل الرياضية، فإننا لن نستطيع أن نحسم مسائل عديدة في حياتنا اليومية. وسنتطرق في هذا المقال إلى سرد مجموعة من المعلومات عن الجذور التربيعية.
تعريف الجذر التربيعي
هو عدد حقيقي ثان، حاصل ضربه في نفسه يعطي الرقم الأصلي، ويرمز للجذر التربيعي ب(√) وتسمى علامة الجذر، وتتميز الجذور التربيعية للعدد المربع بأنّ العدد النسبيّ الموجب مربع، فهو مربع لعددين نسبيين صحيحين إحداهما معكوس الآخر، حيث أنّ كل رقم موجب له جذر تربيعي موجب وسالب، ولا يوجد جذر تربيعي للأعداد السالبة ضمن الأعداد الحقيقية، والجذران التربيعيان دائما لهما القيمة العددية نفسها، مثلا 81؛ الجذر التربيعي الموجب للعدد 81 (81√) +هو= 9، والجذر التربيعي السالب للعدد 81 (81√) – هو = -9.
أول من استخدم الجذر التربيعي
أول من استخدم الجذر التربيعي
إنّ أول من استخدم الجذر التربيعي هو العالم المسلم الرياضي محمد بن موسى الخوارزمي، حيث كان من أوائل علماء الرياضيات وكان لأعماله الدور الكبير في تقدّم الرياضيات، حيث وضع طرق لحساب حجم الهرم الثلاثي وحجم الهرم الرباعي وحجم المخروط، ووضع طريقة لضرب الجذور وقسمتها الذي سيتم توضيحه في هذا المقال. وأول من استعمل الجذر التربيعي للأغراض الحسابية هو العالم أبو الحسن علي بن محمد القلصادي الأندلسي.
العمليات الحسابيّة على الجذور التربيعية
العمليات الحسابيّة على الجذور التربيعية
- ضرب وقسمة جذرين تربيعين: تنص القاعدة على أنّ حاصل ضرب أو قسمة جذرين تربيعيين لعددين يساوي الجذر التربيعي لحاصل ضرب العديين أو قسمة العددين؛ حيث أن أ 0<، ب 0<.
- جمع و طرح جذرين تربيعين
- فإن أ√ x ب√ = بxأ√
- ب√\أ√ = (ب\ أ ) √
- جمع وطرح جذرين تربيعين:
تتم عملية جمع أو طرح الجذور التربيعية بتبسيطها أولا، ثم جمع أو طرح الجذور المتشابهة بعد تبسيطها؛ وتكون الجذور التربيعية متشابهة إذا بقيت العوامل نفسها داخل الجذر التربيعي، ويمكن معرفة إذا كانا الجذران متشابهان عن طريق التحليل إلى العوامل.
- أ√ + ب√ = ب+أ√
- أ√ – ب√ = ب-أ√
أمثلة على العمليات الحسابية
- 45√2+ 125√4
- الحل:
- 5√*20=5√*4*5=25*5√4=125√4
- 5√*6=5√*3*2=5*9√2=45√2
- 5√20 +5√6=
- 5√26=
- 25√*4√
- الحل:
- 4*25√=
- 100√=
- 10=
إظهار التوقيع
توقيع : هبه شلبي
التوقيع لا يظهر للزوار ..
رد: الجذور التربيعية ، تعرف على الجذور التربيعية ، معلومات عن الجذور التر
إظهار التوقيع
توقيع : مريم 2
التوقيع لا يظهر للزوار ..
رد: الجذور التربيعية ، تعرف على الجذور التربيعية ، معلومات عن الجذور التر
إظهار التوقيع
توقيع : حنين الروح123
التوقيع لا يظهر للزوار ..
الساعة الآن 03:04 PM
جميع المشاركات تمثل وجهة نظر كاتبها وليس بالضرورة وجهة نظر الموقع